動物の個体数に関する分析は数学的・統計学的に求められます。
その中で生物群集の解析方法の1つとして、「元村の法則」が用いられることがあります。
生物群集が構造的規則性を示す最も簡単な事例であり、頻出する内容です。
元村の法則(元村の等比級数法則:motomura’s law of geometric series)
元村の法則(元村の等比級数法則:motomura’s law of geometric series)は、1932年に元村勲が『群集の統計的取扱に就いて』で発表した、動物群集の「等比級数則(geometric series)」のことです。
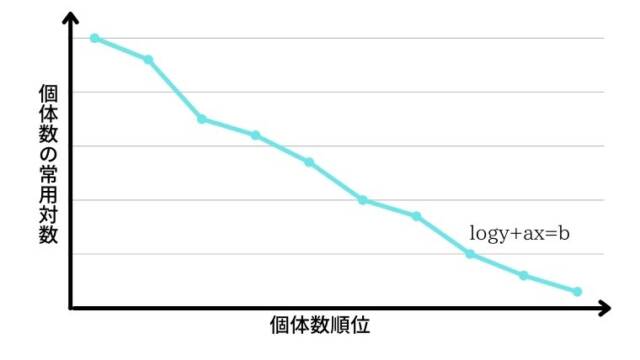
種と個体数との関係について、個体数をy、群集における個体数の順位をxとすると以下の式が成り立ちます。
logy+ax=b(a、bは定数)
縦軸に個体数の対数、個体数の順位を横軸にプロットしていくと、綺麗な右肩下がりの直線になります。
この法則を用いることで以下の3点がわかります。
- 「個体数の多い種は少なく、個体種の少ない種は多い」ということ。
- グラフの傾き1/aが緩やかであるほど群集内の種数が多いことを示すため、「1/a」が群集の多様性の指数として使える。
- 発見できない希少種を含めた群集総個体数を推定できる。
この法則について解説した論文が2012年にOikosに掲載されました。
まとめ

元村の法則(元村の等比級数法則)について、まとめました。
生態学についてより深く勉強するのに、おすすめの書籍をまとめていますのでご参照ください。